该公告已过公示时间，对该公告内容进行下架处理，给您带来的不便敬请谅解。
【试题练习】
某单位有两个订单，分别是制作桌子和椅子，目前2名工匠师傅参与制作。若桌子的订单由甲师傅单独完成需要24天，若由乙师傅单独完成需要36天；若椅子的订单由甲师傅和乙师傅合作完成需要20天，若由甲师傅单独完成需要60天。现有新的订单，桌子数量翻一番，椅子数量不变，则甲、乙合作完成需要的最短时间为（ ）天。（不足一天按一天计算）
A.39
B.40
C.41
D.42
正确答案：C
【解析】第一步，本题考查工程问题中的时间类。
第二步，根据甲、乙师傅完成桌子订单的时间，给桌子的总量赋值为24和36的最小公倍数72，可得甲、乙师傅做桌子的效率分别为3和2；同理，给椅子的总量赋值为20和60的最小公倍数60，可得甲、乙师傅做桌子的效率和为3，甲师傅做桌子的效率为1，则乙师傅的效率为3－1=2。由此可知甲师傅擅长做桌子，乙师傅擅长做椅子。
第三步，求甲、乙合作完成需要的最短时间，则需要让擅长的人做擅长的事情。新的订单桌子数量翻一番，是72×2=144，椅子数量不变，是60。乙师傅完成椅子订单的时间为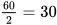
天，这30天中甲师傅完成桌子的量为30×3=90，余下的可由甲乙两人合作制作，还需要的时间为
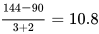天，即11天。故完成总订单的时间为30＋11=41天。
因此，选择C选项。
（编辑：huqiao01）
