该公告已过公示时间,对该公告内容进行下架处理,给您带来的不便敬请谅解。
【试题练习】
每年三月某单位都要组织员工去A、B两地参加植树活动。已知去A地每人往返车费20元,人均植树5棵,去B地每人往返车费30元,人均植树3棵,设到A地员工有x人,A、B两地共植树y棵,y与x之间满足y=8x-15,若往返车费总和不超过3000元,那么,最多可植树多少棵?
A.489
B.400
C.498
D.500
正确答案:A
【解析】解法一:
第一步,本题考查函数问题。
第二步,A地人均5棵,则在A地植树5x,根据总植树棵数y=8x-15,可得B地植树棵数为(8x-15)-5x=3x-15,则B地人数为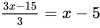 (人)。
(人)。
第三步,为了植树最多,则投入费用需要最高,根据不超过3000元,可得总费用3000≥20x+30(x-5),解得x≤63。
第四步,当x=63时,最多可植树y=8×63-15=489(棵)。
因此,选择A选项。
解法二:
第一步,本题考查函数问题,用数字特性法解题。
第二步,植树棵数y=8x-15,根据奇偶特性,8x是偶数,15是奇数,故可推出y一定为奇数。
因此,选择A选项。

(编辑:longyan01)


